Projet Rootlocker
Présentation
Rootlocker est un algorithme permettant de chercher toutes les racines d'une équation holomorphe du type f(z)=0 dans une portion du plan complexe définie par l'utilisateur.
Aujourd'hui, deux implémentations de cet algorithme existent :
- La première, réalisée en Java durant mes années de thèse, comporte une interface graphique simplifiant grandement son utilisation. Elle peut être téléchargée ici :
 .
.
- La seconde, réalisée en Python (2.x) possède un code source beaucoup plus concis et ne dispose pas d'interface graphique associée. Cette dernière peut être obtenue directement sous pypi ici .
Le code décrivant la fonction f(z) étant appelé de très nombreuses fois (parfois plus de 20 000 fois en présence d'un nombre important de racines), il convient de l'écrire de manière optimisée ! Son écriture dans un langage compilé (C) a été testé et permet une résolution jusqu'à 100 fois plus rapide !
Pour finir, voici un article détaillé (en anglais) décrivant le fonctionnement de l'algorithme et présentant différents cas tests. Cet article est un extrait (le chapitre 2) de mon manuscrit de thèse réalisé au laboratoire de L'IMFT à Toulouse sous la direction de Thierry Poinsot et Laurent Selle.
Utilisation
Interface graphique
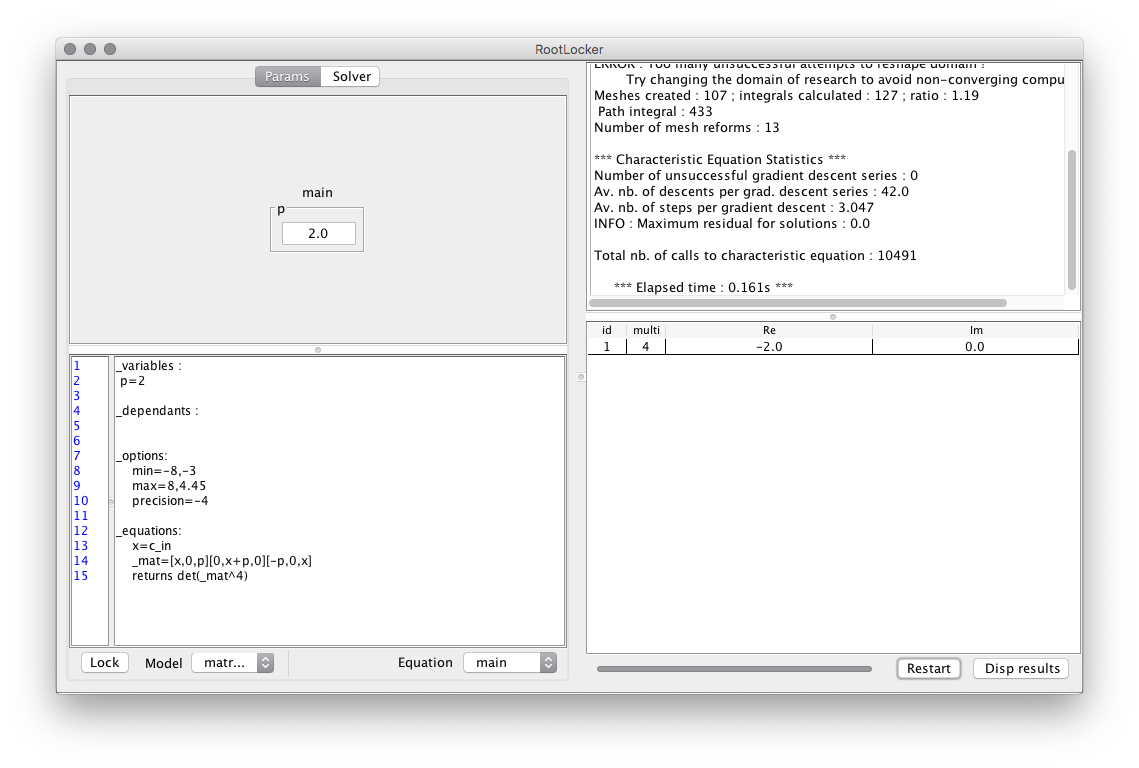
L'équation à résoudre doit être spécifiée dans un fichier .stj qui peut être directement créé, modifié et affiché à partir de l'interface en bas à gauche. Une fois le fichier écrit, il peut être chargé (en pratique, l'équation sera convertie en un fichier JAVA et chargée automatiquement par l'interface). Une fois le fichier chargé, certains paramètres peuvent s'afficher dans la partie en haut à gauche de l'interface. Il s'agit de paramètres apparaissant dans l'équation à résoudre et dont les valeurs peuvent ainsi être modifiées sans avoir à recharger le modèle.
La résolution est déclenchée lors de l'appui sur le bouton Restart. Les résultats (solutions et ordre de multiplicité) s'affichent dans la partie en bas à droite tandis que les statistiques liées à la résolution s'affichent en haut à droite de l'interface. Les résultats peuvent être visualisés sur un graphique en cliquant sur le bouton Disp results.
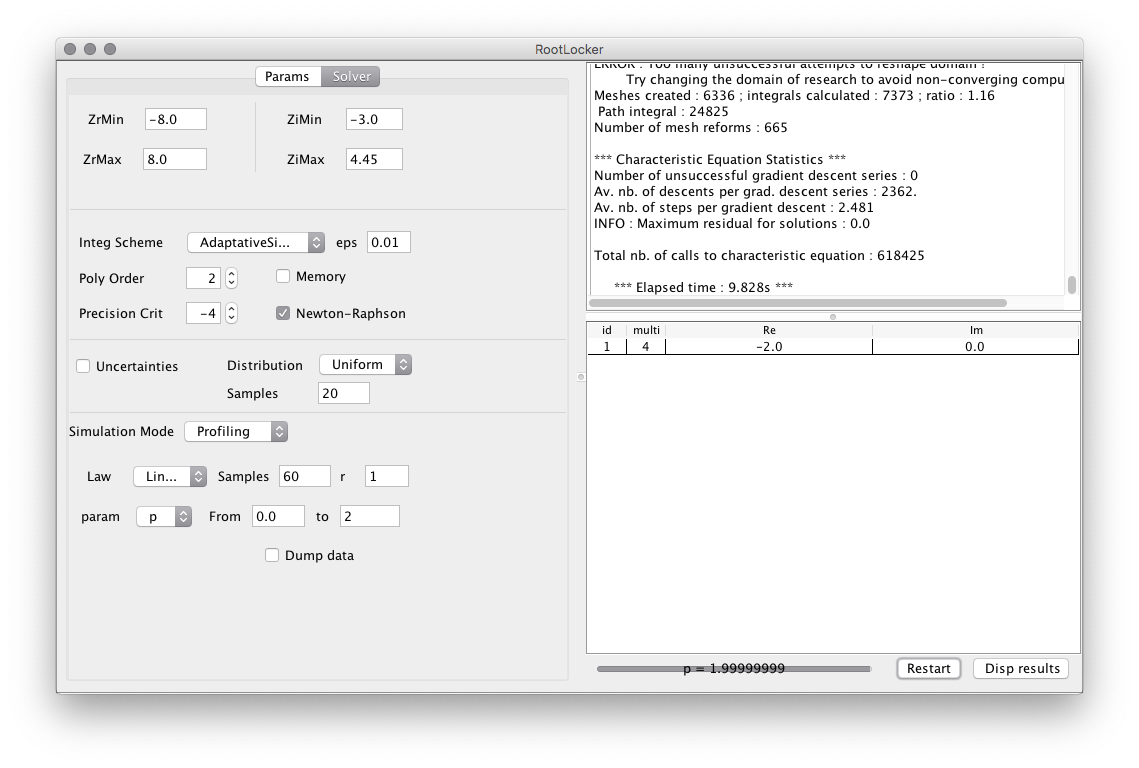
L'onglet de réglage permet de modifier les paramètres de résolution (intégration numérique, utilisation ou non de la méthode de Newton pour améliorer la précision, ...) ainsi que le choix du mode de résolution :
- Simple : c'est le mode par défaut. Les solutions sont recherchées à l'aide de la méthode décrite dans cette page.
- Profiling : plusieurs résolutions simples sont réalisée pour différentes valeurs d'un paramètre. Les solutions sont ensuite regroupées par famille.
- Tracking : Similaire au profiling mais la résolution complète est uniquement réalisée pour la première valeur du paramètre. Pour les valeurs ultérieures, seule la méthode de Newton-Raphson est utilisée. Le tracking est donc beaucoup plus rapide que le profiling mais ne garantis pas que toutes les solutions soient obtenues.
Fichier stl
Le problème à résoudre est décrit dans un fichier texte (d'extension .stj). Ce fichier contient des informations sur les paramètres (ainsi que leurs valeurs par défaut), les réglages (domaine du plan complexe, méthode numérique, ...) et finalement l'équation à résoudre. Un exemple de fichier stl est donné ci-dessous.
_variables : tag obligatoire avant la déclaration de paramètres
p=2 création d'un paramètre nommé p et valant 2 par défaut
_dependants :
pmod=p*p un paramètre dépendant peut dépendre des paramètres non dépendant du modèle et sera mises à jour uniquement lorsqu'un paramètre du modèle est modifié.
_options:
min=-8,-3 origine du repère (partie réelle , partie imaginaire)
max=8,4.45
precision=-4 précision attendue lors de la recherche des solutions, ici 10^-4
_equations:
x=c_in c_in est la variable d'entrée (qui peut être renommée pour plus de commodité)
_mat=[x,0,p][0,x+p,0][-pmod,0,x] une variable de type matrice doit avoir un nom du type _***
returns det(_mat^4) renvoie f(c_in) tel que le problème à résoudre soit f(c_in)=0
Ce langage, bien que simple, permet de décrire de nombreuses équations à résoudre, que ces dernières soient scalaires ou linéaires.
Théorie
L'algorithme RootLocker est basé sur l'utilisation récursive d'une généralisation du principe de l'argument :
Ainsi, le calcul de cette intégrale sur un contour fermé permet d'obtenir les sommes (à la puissance k) des solutions z i présente à l'intérieur du contour. Le nombre de solutions Nsol est obtenu pour k=1.
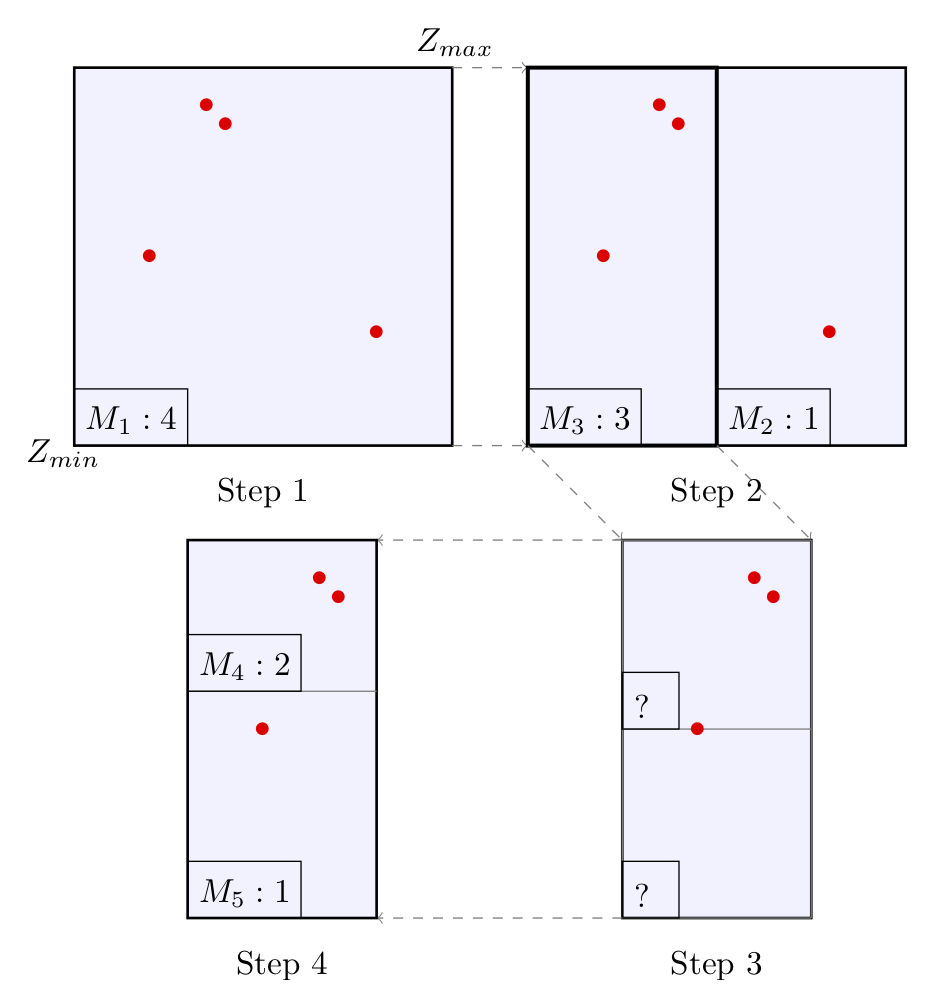
Si ce dernier est trop grand (i.e >3), le domaine délimité par le contour est subdivisé en deux sous-domaine et l'algorithme se poursuit de manière récursive.
Lorsque Nsol est inférieur ou égal à 3. On peut former un polynôme à partir des sommes des z i à la puissance k et dont les racines sont égales aux z i . Ce polynôme est ensuite résolu de manière exacte.
La précision des résultats obtenus dépend directement du critère d'arrêt utilisé pour le calcul des intégrales. Plus les intégrales sont calculées précisément, plus les résultats obtenus sont proches des solutions du problème initial. Afin toutefois d'améliorer singulièrement la précision des résultats (avec un très léger surcout en calcul), la méthode de Newton-Raphson est ensuite utilisée à partir de chaque solution approchée obtenue.
La méthode de Simpson adaptative est utilisée pour le calcul des intégrales et les dérivées sont obtenues de manière exacte à l'aide de l'utilisation d'un outil de différentiation automatique .
- Lorsqu'une solution se trouve sur le contour d'un domaine (ou très proche), le calcul de l'intégrale ne converge pas. Lorsque cette situation est détectée, le domaine parent (s'il existe) est découpé différemment comme montré entre les étapes 3 et 4 du schéma ci-dessus.
- D'un point de vue numérique, deux solutions très proches l'une de l'autre se comportent comme une solution d'ordre 2. Tout groupe de p solutions suffisamment proches les unes des autres est considéré comme une unique solution d'ordre de multiplicité p. La méthode de Newton-Raphson prend en compte cet ordre de multiplicité afin de converger plus rapidement.